Conductivité thermique

Cette page présentera un protocole possible de mesure de la conductivité thermique ainsi que les résultats obtenus pour un exemple d'échantillon. Les résultats de la mesure effectuée seront placés dans l'onglet "Data". Une page Wikipédia est entièrement consacrée au phénomène de conductivité thermique que vous pouvez retrouver via le portail Conductivité thermique

Définition de la conductivité thermique

La conductivité thermique est une propriété physique traduisant la capacité d'un matériau à transférer la chaleur par unité de surface et de temps sous un gradient de température de 1 kelvin ou de 1 degré Celsius par mètre et ce, sans déplacement macroscopique de matière. Elle peut se noter λ, $\kappa$ ou k et s'exprime en W.m^-1.K^-1. Pour un matériau homogène et isotrope, la conductivité thermique se retrouve classiquement dans la loi de Fourier en reliant la densité de flux de chaleur au gradient de température comme ci-dessous :

${\vec {\varphi }}=-\lambda \,{\overrightarrow {\operatorname {grad} }}\,T$

où :

${\vec {\varphi }}\,$ désigne la densité de flux de chaleur (W/m²),

λ la conductivité thermique (W.m^-1.K^-1),

${\overrightarrow {\operatorname {grad} }}\,$ l'opérateur gradien,

T la température (K).

Lorsque le matériau est anisotrope, sa conductivité thermique varie selon les directions. Le λ mentionné dans la loi de Fourier peut alors s'exprimer par un tenseur de conductivité :

λ = ${\begin{Vmatrix}\lambda _{1,1}&\lambda _{1,2}&\lambda _{1,3}\\\lambda _{2,1}&\lambda _{2,2}&\lambda _{2,3}\\\lambda _{3,1}&\lambda _{3,2}&\lambda _{3,3}\end{Vmatrix}}$

Avec les remarques suivantes :

• $\lambda _{i,j}$ > 0
• $\lambda _{i,j}$ = $\lambda _{j,i}$
• $\lambda _{i,i}\lambda _{j,j}-\lambda _{i,j}^{2}>0$

Or, en définissant les axes de coordonnées selon des directions particulières, de simplifier le tenseur de conductivité en annulant tous les coefficients de la matrice qui ne sont pas des coefficients diagonaux. Le λ de la loi de Fourier s'exprime alors de la manière suivante :

λ = ${\begin{Vmatrix}\lambda _{1,1}&0&0\\0&\lambda _{2,2}&0\\0&0&\lambda _{3,3}\end{Vmatrix}}$

Dans le cas très répandu d'un transfert de chaleur à travers une paroi d’épaisseur e dont les deux faces planes de surface S sont maintenues aux températures T1 et T2, avec T2 > T1), le flux de chaleur Φ (quantité de chaleur traversant le mur) en régime permanent s'exprime de la manière suivante :

$\Phi =\lambda \,{\frac {S}{e}}\,(T_{2}-T_{1})$

Avec :

Φ en W,

λ en W.m^-1.K^-1,

e en m,

S en m²,

T₁, T₂ en K.

Protocole de mesure de la conductivité thermique par la méthode de l'état stationnaire

Il existe plusieurs méthodes de mesure de la conductivité thermique d’un matériau comme les méthodes 3ω , la méthode Flash ou les méthodes calorimétriques. Les mesures proposées sur cette page ont été réalisées par la méthode de l’état stationnaire qui permet des mesures d’une grande précision dans l’intervalle de température 5 – 300 K. La technique est dite « méthode de l’état stationnaire » car les mesures sont réalisées quand le système est à l’équilibre thermique ou lorsque le gradient de température est stable. Montage 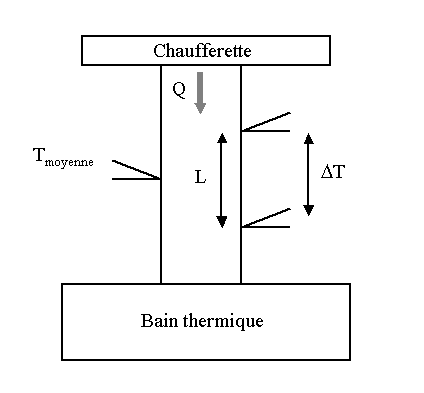L’une des extrémités de l’échantillon de section A est fixée à un porte-échantillon (puit thermique) dont le rôle est d'évacuer le flux thermique traversant l'échantillon, et l’extrémité opposée à une chaufferette dissipant dans l’échantillon une puissance thermique Q obtenue par effet Joule, de manière à créer un gradient thermique le long de l’échantillon. Des thermocouples séparés par une distance L mesurent la différence de température ΔT le long de l’échantillon. Un troisième thermocouple, calibré, est également fixé à l’échantillon pour déterminer sa température moyenne (la température de mesure). La conductivité thermique est alors donnée par : λ ={\tfrac {Q\times L}{A\times \Delta T}}}

Sources d’erreurs

La précision de la mesure dépend des pertes thermiques. Celles-ci peuvent avoir plusieurs origines comme la conduction thermique par les fils des thermocouples, la convection du gaz résiduel, les radiations par les surfaces de l’échantillon ou les pertes dans la chaufferette. Afin de minimiser ces pertes, il convient de prendre certaines dispositions comme cela a été fait pour les résultats de mesure qui sont proposés sur cette page. Le système de mesure et l’échantillon sont placés dans une chambre de mesure sous vide (~10-6 mbar) afin de minimiser les pertes par convection. Cette chambre est elle-même enveloppée dans plusieurs boucliers thermiques dont la température est régulée (afin de minimiser les effets radiatifs). Enfin, les fils des thermocouples sont choisis de manière à conduire le moins possible la chaleur, il faut dans l’idéal qu’ils soient les plus longs et les plus fins possibles pour augmenter la résistance thermique des fils. Plus la température augmente et plus il est difficile de minimiser toutes ces pertes. Cette méthode de mesure à l’état stationnaire ne permet la mesure de la conductivité thermique qu’à des températures inférieures à la température ambiante.